Lorsque l'on réalise des tests statistiques "à la main", c'est-à-dire en appliquant soi-même des formules, par opposition à l'utilisation d'un logiciel de statistiques qui contient des formules pré-programmées, on calcule une certaine statistique (par exemple le t de student ou le

), qu'il faut ensuite convertir en valeur
p pour prendre une décision.
Dans la plupart des cas, il n'y a pas de formule simple pour calculer ces valeurs
p et l'on va donc utiliser des tables permettant la conversion entre certaines valeurs que peut prendre la statistique
t calculée et les valeurs
p. requises pour la décision statistique. On recourt alors à des tables dont on explique ici l'utilisation.
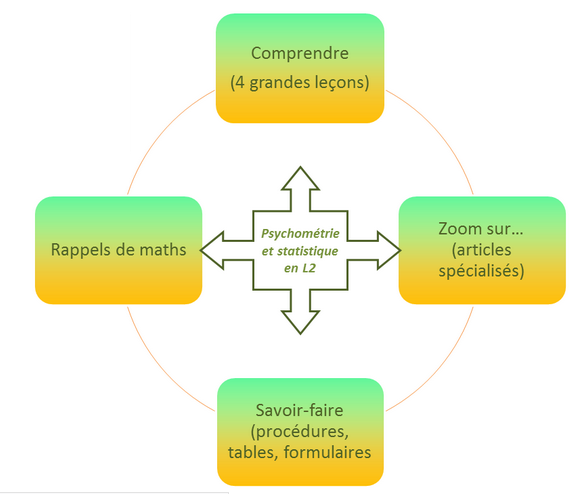 Ce module de niveau L2 de psychologie est organisé en quatre parties :
Ce module de niveau L2 de psychologie est organisé en quatre parties :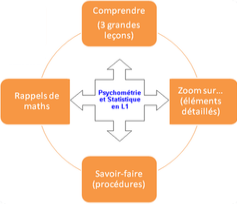

 Cette grande leçon introduit la statistique inférentielle et la psychométrie appliquée, ceci dans la perspective de permettre aux étudiants de comprendre les enjeux épistémologiques, scientifiques et techniques de ces matières. Ces enjeux comprennent en particulier la mise au point de méthodes objectives pour l’étude de la variabilité induite expérimentalement ou observée en condition naturelle.
Cette grande leçon introduit la statistique inférentielle et la psychométrie appliquée, ceci dans la perspective de permettre aux étudiants de comprendre les enjeux épistémologiques, scientifiques et techniques de ces matières. Ces enjeux comprennent en particulier la mise au point de méthodes objectives pour l’étude de la variabilité induite expérimentalement ou observée en condition naturelle.
 Le titre développé de cette grande leçon est « Du qualitatif au quantitatif : théorie et applications ». Consacrée à la psychométrie, elle approfondit la problématique de la mesure en psychologie selon deux perspectives.
Le titre développé de cette grande leçon est « Du qualitatif au quantitatif : théorie et applications ». Consacrée à la psychométrie, elle approfondit la problématique de la mesure en psychologie selon deux perspectives.  Cette grande leçon introduit les principales stratégies permettant de comparer des moyennes par rapport à une valeur de référence ou des moyennes entre elles.
Le
Cette grande leçon introduit les principales stratégies permettant de comparer des moyennes par rapport à une valeur de référence ou des moyennes entre elles.
Le  Cette grande leçon présente, sous l'angle de la statistique inférentielle, les principales méthodes pour tester l'existence d'une association entre variables : corrélations de variables numériques (r
de Pearson) ordinales (
Cette grande leçon présente, sous l'angle de la statistique inférentielle, les principales méthodes pour tester l'existence d'une association entre variables : corrélations de variables numériques (r
de Pearson) ordinales (




 Objectifs : Cette section comporte un ensemble de tutoriels visant à montrer comment réaliser concrètement des tests de comparaison de moyennes à deux groupes (t de student et Welch) ou plus (ANOVA) avec des logiciels...
Objectifs : Cette section comporte un ensemble de tutoriels visant à montrer comment réaliser concrètement des tests de comparaison de moyennes à deux groupes (t de student et Welch) ou plus (ANOVA) avec des logiciels... Objectifs. Cette section comporte un ensemble de vidéos montrant comment comparer deux groupes lorsqu'un test paramétrique n'est pas utilisable, par exemple lorsque la distribution normale n'est pas respectée ou que la variable dépendante est seulement ordinale.
Objectifs. Cette section comporte un ensemble de vidéos montrant comment comparer deux groupes lorsqu'un test paramétrique n'est pas utilisable, par exemple lorsque la distribution normale n'est pas respectée ou que la variable dépendante est seulement ordinale.